青书学堂信阳师范计算方法网上考试答案
| 辛甫生(Simpson)求积公式的代数精确度为( )。 |
| A:1 B:2 C:3 D:4 |
|
| 二分法又称为( )。 |
| A:对分法 B:差分法 C:迭代法 D:反幂法 |
|
| 弦截法是作( )的方程。 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
| 牛顿法是作( )的方程。 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
| 牛顿插值多项式可用于( )任意分布的情况。 |
| A:节点 B:峰值 C:均值 D:差值 |
|
| 牛顿插值多项式的计算公式可用( )进行简化。 |
| A:差分 B:迭代 C:高斯消去法 D:反幂法 |
|
| 牛顿插值多项式的特例是指( )。 |
| A:等距节点插值多项式 B:非等距节点插值多项式 C:插值多项式 D:赛德尔迭代格式 |
|
| SOR方法是将( )稍加改进而得到的一种加速迭代法。 |
| A:赛德尔迭代格式 B:牛顿迭代格式 C:等距节点插值多项式 D:非等距节点插值多项式 |
|
| 直接法也叫( )。 |
| A:精确法 B:精准法 C:精度法 D:二分法 |
|
| “将非线性方程f(X) =0逐步转化为线性方程来求解”,这说的是以下什么方法的基本思想?( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:牛顿迭代法 |
|
“通过计算隔根区间的中点,逐步将隔根区间缩小,从而得方程的近似根数列 ”的是什么方法的基本思想?( ) ”的是什么方法的基本思想?( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
“把方程f(x)=0化为等价方程x=φ(x),得迭代公式 ,用该公式反复迭代,得方程的近似根数列”指的是( ) ,用该公式反复迭代,得方程的近似根数列”指的是( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
| “画出y=f(x)的简图,从曲线与x轴交点的位置确定出隔根区间,或者将方程等价变形为g1(x)=g2(x),画出函数y=g1(x)和y=g2(x)的简图,从两条曲线交点的横坐标的位置确定隔根区间”的方法是( )。 |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
拉格朗日差值多项式中,称 为关于差值基点 为关于差值基点 的差值基函数,则以下各式正确的是。( ) 的差值基函数,则以下各式正确的是。( ) |
A: B: B:   C: C:  D: D:   |
|
若要使用顺序高斯消去法求解方程组 ,顺序消元过程能进行到底的充要条件是系数矩阵A满足( )。 ,顺序消元过程能进行到底的充要条件是系数矩阵A满足( )。 |
A:A的各阶顺序主子式不为零 B: 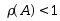 C: C:  D: D:  |
|
已知方程 在 在 内有一实根,现在把方程写成以下两种不同的等价式, 内有一实根,现在把方程写成以下两种不同的等价式, ,对于每个等价式对应的迭代公式在x0=1.5附近的敛散性,下面哪种说法正确?( ) ,对于每个等价式对应的迭代公式在x0=1.5附近的敛散性,下面哪种说法正确?( ) |
| A: (1)发散(2)收敛 B: (1)发散(2)发散 C: (1)收敛(2)收敛 D: (1)收敛(2)发散 |
|
若近似值 精确到 精确到 ,则 ,则 的绝对误差限是( )。 的绝对误差限是( )。 |
A: B: B: C: C: D: D: |
|
| 取3.1415为圆周率π的近似值,则该近似值具有( )位有效数字。 |
| A: 5 B: 4 C: 3 D: 2 |
|
设 ,均差 ,均差 =( ) =( ) |
| A:3 B: 5 C: -6 D:0 |
|
函数 的n次差值多项式 的n次差值多项式 的余项为( )。 的余项为( )。 |
A: B: B: C: C: D: D: |
|
有下列数表所确定的插值多项式的次数是( )。

|
| A:二次; B:三次; C:四次; D:五次 |
|
 ,范数‖x‖2是( ). ,范数‖x‖2是( ). |
A: B:27 C:9 D:8 B:27 C:9 D:8 |
|
| 对解方程组的Jacobi迭代法和Seidel迭代法,下例说法正确的是( ). |
| A:存在一者收敛,一者发散 B:Jacobi迭代法收敛速度快一些 C:两者同时收敛 D:Seidel迭代法收敛速度快一些 |
|
 是给定的互异节点, 是给定的互异节点, 是以它们为插值节点的插值多项式,则 是以它们为插值节点的插值多项式,则 是一个( ). 是一个( ). |
| A:次数不超过n的多项式 B:n次多项式 C:次数小于n的多项式 D:n+1次多项式 |
|
在解方程组 中,下列哪种方法属于直接法:( ) 中,下列哪种方法属于直接法:( ) |
| A:雅格比法 B:列主元消元法 C:sor法 D:gauss-seidel法 |
|
| 已知自然数e=2.718281828459045…,取e≈2.71828,那么e具有的有效数字是( ) |
| A:5位 B:6位 C:7位 D:8位 |
|
 |
| A: 1 B: 2 C:3 D: 4 |
|
 |
| A:1 B: 2 C: 3 D: 4 |
|
 |
| A: 1 B: 2 C: 3 D:4 |
|
 |
A: B: X=1.3315 C: X=1.3125 D: X=3.125 B: X=1.3315 C: X=1.3125 D: X=3.125 |
|
| 下列方程表述正确的是( )。 |
A:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: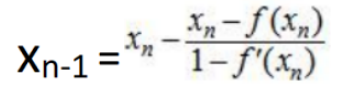 C:x=cosx根的牛顿迭代公式是: C:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: |
|
| 关于方程cosx+sinx-4x=0,有如下说法,正确的是( )。 |
A:该方程的有一个根 B:该方程的有二个根 C:隔根区间为[0,π/4] D:收敛的迭代公式为: |
|
| 下列计算结果正确的是( )。 |
A:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04476 B:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04476 B:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04000 C:用迭代法求方程 的正根,准确到小数点后第5位的值为:a≈1.04000 C:用迭代法求方程 的根,要求精度为 的根,要求精度为 的值为:a≈0.0905 D:用迭代法求方程 的值为:a≈0.0905 D:用迭代法求方程 的根,要求精度为 的根,要求精度为 的值为:a≈0.0900 的值为:a≈0.0900 |
|
方程 在1.5附近有根,把方程写成4种不同的等价形式,并建立相应的迭代公式,具体如图,则判断每种迭代公式产生的数列在1.5附近的收敛性,正确的是( )。 在1.5附近有根,把方程写成4种不同的等价形式,并建立相应的迭代公式,具体如图,则判断每种迭代公式产生的数列在1.5附近的收敛性,正确的是( )。
 |
| A:(1)收敛 B:(2)收敛 C:(3)发散 D:(4)发散 |
|
| 下列关于偏微分方程的数值解法的说法正确的有( )。 |
| A:偏微分方程定解问题的数值解法之一是差分解法 B:偏微分方程定解问题的数值解法之二是有限元方法 C:差分解法的基本思想是:在偏微分方程中,用差商(均差)代替偏导数,把偏微分方程定解问题转化为求解线性代数方程问题,从而得到定解问题的解函数在离散点的近似值 D:线性代数方程称为差分方程,差分方程的解称为偏微分方程定解问题的数值解. |
|
| 雅可比方法的主要特点是什么? |
| A:算法稳定 B:精度高 C:求得的特征向量正交性好 D: 稀疏性 |
|
| 在科学与工程计算中,估计计算结果的精确度是十分重要的工作,而影响精确度的因素是各种各样的误差.按照它们的来源,误差可以分为以下哪几种?( ) |
| A:模型误差 B:观测误差 C:截断误差 D:舍入误差 |
|
| 按照一般的情况,指出选用算法时应遵循的一般原则是( )。 |
| A:要尽量简化计算步骤以减少运算次数 B:要防止大数“吃掉”小数 C:尽量避免相近的数相减 D:除法运算中应尽量避免除数的绝对值远远小于被除数的绝对值 E:选用数值稳定性好的公式,以控制舍入误差的传播 |
|
| 求隔根区间的方法有( )。 |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
设为区间[a,b]上的连续函数,且已知点 上的函数值为 上的函数值为 ,若存在一个简单函数φ(x),使 ,若存在一个简单函数φ(x),使 ,则下列说法正确的是( )。 ,则下列说法正确的是( )。 |
A:φ(x)称为f(x)的插值函数,f(x) 称为被插值函数 B:点 称为插值节点 C:条件 称为插值节点 C:条件 称为插值条件 D:所在区间[a,b]称为插值区间,求插值函数φ(x)的问题(方法)称为插值问题(方法) 称为插值条件 D:所在区间[a,b]称为插值区间,求插值函数φ(x)的问题(方法)称为插值问题(方法) |
|
设初值问题
(1)写出求上述初值问题数值解的显式Euler公式;
(1)写出求上述初值问题数值解的梯形公式;
(2)写出求上述初值问题数值解的改进Euler公式. |
|
|

