青书学堂信阳师范计算方法(直播)网上考试答案
一节点的Gauss-Legendre求积公式计算积分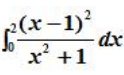 的近似值为( )。 的近似值为( )。 |
| A:0 B:1 C:2 D:3 |
|
积公式 的代数精度为( )。 的代数精度为( )。 |
| A:1 B:2 C:3 D:5 |
|
积公式 的代数精度为( )。 的代数精度为( )。 |
| A:1 B:2 C:3 D:5 |
|
| 线性方程组的数值解法有( )。 |
| A:直接法和迭代法 B:直接法和二分法 C:反幂法和乘幂法 D:差分法迭代法 |
|
| ( )是在理论上没有舍入误差的前提下经过有限步运算即可得到方程组的精确解。 |
| A:直接法 B:迭代法 C:差分法 D:高斯消去法 |
|
| ( )是对增广矩阵(A|b)进行一系列的初等行变换。 |
| A:差分法 B:反幂法 C:乘幂法 D:高斯消去法 |
|
| ( )主要用来求矩阵的主特征值(按模最大的特征值)及相应的特征向量。 |
| A:反幂法 B:差分法 C:乘幂法 D:直接法 |
|
| 乘幂法也是一种( )法。 |
| A:差分 B:迭代 C:二分 D:直接法 |
|
| ( )可用来求矩阵的按模最小的特征值及相应的特征向量。 |
| A:反幂法 B:差分法 C:乘幂法 D:二分法 |
|
| 辛甫生(Simpson)求积公式的代数精确度为( )。 |
| A:1 B:2 C:3 D:4 |
|
| 二分法又称为( )。 |
| A:对分法 B:差分法 C:迭代法 D:反幂法 |
|
| 弦截法是作( )的方程。 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
| 牛顿法是作( )的方程。 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
| 牛顿插值多项式可用于( )任意分布的情况。 |
| A:节点 B:峰值 C:均值 D:差值 |
|
| 牛顿插值多项式的计算公式可用( )进行简化。 |
| A:差分 B:迭代 C:高斯消去法 D:反幂法 |
|
| 牛顿插值多项式的特例是指( )。 |
| A:等距节点插值多项式 B:非等距节点插值多项式 C:插值多项式 D:赛德尔迭代格式 |
|
| SOR方法是将( )稍加改进而得到的一种加速迭代法。 |
| A:赛德尔迭代格式 B:牛顿迭代格式 C:等距节点插值多项式 D:非等距节点插值多项式 |
|
| 直接法也叫( )。 |
| A:精确法 B:精准法 C:精度法 D:二分法 |
|
| “将非线性方程f(X) =0逐步转化为线性方程来求解”,这说的是以下什么方法的基本思想?( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:牛顿迭代法 |
|
n阶矩阵 称为严格对角占优阵是指矩阵元素满足( )。 称为严格对角占优阵是指矩阵元素满足( )。 |
A:  B: B: C: C:   D: D: |
|
设矩阵A= ,那么以A为系数矩阵的线性方程组AX=b的雅可比迭代矩阵为( )。 ,那么以A为系数矩阵的线性方程组AX=b的雅可比迭代矩阵为( )。 |
A:  B: B:  C: C:  D: D:  |
|
已知 ,则 ,则 ( )。 ( )。 |
| A: 1.2 B: 0.2 C: 0.7 D: 0.6 |
|
 |
| A: 1 B: 2 C:3 D: 4 |
|
 |
| A:1 B: 2 C: 3 D: 4 |
|
 |
| A: 1 B: 2 C: 3 D:4 |
|
 |
A: B: X=1.3315 C: X=1.3125 D: X=3.125 B: X=1.3315 C: X=1.3125 D: X=3.125 |
|
在牛顿-柯特斯求积公式: 中,当系数 中,当系数 是负值时,公式的稳定性不能保证,所以实际应用中,当( )时的牛顿-柯特斯求积公式不使用。 是负值时,公式的稳定性不能保证,所以实际应用中,当( )时的牛顿-柯特斯求积公式不使用。 |
A: , B: , B: , C: , C: , D: , D: , , |
|
若用二阶中点公式 求解初值问题 求解初值问题 ,试问为保证该公式绝对稳定,步长 ,试问为保证该公式绝对稳定,步长 的取值范围为( )。 的取值范围为( )。 |
A: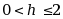 , B: , B: , C: , C: , D: , D: |
|
解方程组 的简单迭代格式 的简单迭代格式 收敛的充要条件是( )。 收敛的充要条件是( )。 |
A: , B: , B: , C: , C: , D: , D: |
|
| 下列方程表述正确的是( )。 |
A:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: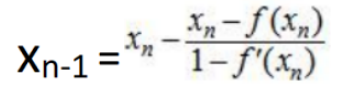 C:x=cosx根的牛顿迭代公式是: C:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: |
|
| 取“355/113”作为π的近似值,则下列计算结果正确的是( )。 |
A:绝对误差为: B:相对误差为: B:相对误差为: C:有效数字为:7位 D:有效数字为:6位 C:有效数字为:7位 D:有效数字为:6位 |
|
| 取“22/7”作为π的近似值,则下列计算结果正确的是( )。 |
A:绝对误差为: B:相对误差为: B:相对误差为: C:有效数字为:3位 D:有效数字为:2位 C:有效数字为:3位 D:有效数字为:2位 |
|
| 取“3.15”作为π的近似值,则下列计算结果正确的是( )。 |
A:绝对误差为: B:相对误差为: B:相对误差为: C:有效数字为:1位 D:有效数字为:2位 C:有效数字为:1位 D:有效数字为:2位 |
|
| 下列关于偏微分方程的数值解法的说法正确的有( )。 |
| A:偏微分方程定解问题的数值解法之一是差分解法 B:偏微分方程定解问题的数值解法之二是有限元方法 C:差分解法的基本思想是:在偏微分方程中,用差商(均差)代替偏导数,把偏微分方程定解问题转化为求解线性代数方程问题,从而得到定解问题的解函数在离散点的近似值 D:线性代数方程称为差分方程,差分方程的解称为偏微分方程定解问题的数值解. |
|
| 若某一数值方法的局部截断误差为Rn=O(hp+1),p为正整数,则称这个数值方法为p阶方法,或者说该方法具有p阶精度,根据这个定义,可以知晓的是( )。 |
| A:欧拉方法是一阶方法 B:欧拉方法是二阶方法 C:梯形法是二阶方法 D:欧拉预估-校正法是二阶方法 |
|
| 下列关于局部截断误差和整体截断误差的说法正确的是( )。 |
A:局部与整体截断误差是方法的理论误差 B:欧拉法的局部截断误差为 C:梯形法的局部截断误差为 C:梯形法的局部截断误差为 D:除了用数值积分方法推导局部截断误差外,泰勒展开方法也是推导局部截断误差的常用方法 D:除了用数值积分方法推导局部截断误差外,泰勒展开方法也是推导局部截断误差的常用方法 |
|
| 雅可比方法的主要特点是什么? |
| A:算法稳定 B:精度高 C:求得的特征向量正交性好 D: 稀疏性 |
|
 以下答案中那几项是正确的? 以下答案中那几项是正确的? |
A: B: B: C: C: D: D: |
|
| 议程的近似方法有 |
| A:二分法 B:迭代法 C:牛顿法 D:弦截法 |
|
确定求积公式 的待定参数,使其代数精度尽量高,并确定其代数精度.利用此公式计算积分 的待定参数,使其代数精度尽量高,并确定其代数精度.利用此公式计算积分 . . |
|
|

