| |
|
QQ:3446094242 |
|
|
微信号:goodluckgold |
|
| 课件学习、网上考试答案,如有需要,请加微信或QQ,全程辅导,为您排忧解难!!! |
|
|
|
|
| |
|
|
青书学堂中原工学院工程数学网上考试答案
若线性方程组 的增广矩阵 的增广矩阵 经过初等行变换化为 经过初等行变换化为 ,则此方程组( ) ,则此方程组( ) |
| A:可能有无穷多解 B:一定有无穷多解 C:可能无解 D:一定无解 |
|
设 都是 都是 阶可逆方阵, 阶可逆方阵, 为单位矩阵,且 为单位矩阵,且 ,则 ,则 =( ) =( ) |
A: B: B:
C: D: D:
|
|
矩阵 的行最简形矩阵是( ) 的行最简形矩阵是( ) |
A:
B:
C:
D:
|
|
设 是非齐次线性方程组 是非齐次线性方程组 的两个不同的解, 的两个不同的解, 是相应的齐次线性方程组 是相应的齐次线性方程组 的基础解系,则 的基础解系,则 的通解为( ) 的通解为( ) |
A:
B:
C:
D:
|
|
若线性方程组 的增广矩阵 的增广矩阵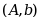 经过初等行变换化为 经过初等行变换化为 ,则此方程组( ) ,则此方程组( ) |
| A:可能有无穷多解 B:一定有无穷多解 C:可能无解 D:一定无解 |
|
设有矩阵 ,则下列运算成立的是( ) ,则下列运算成立的是( ) |
A: B: B: C: C: D: D: |
|
设 ( ) ( ) |
A:
B:
C: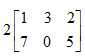
D:
|
|
已知 ,则 ,则 ( ) ( ) |
A: B: B: C: C: 或 或 D: D: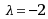 或 或 |
|
已知矩阵 , , 为3阶非零矩阵,且满足 为3阶非零矩阵,且满足 ,则( ) ,则( ) |
A:当 时, 时, 的秩为1 B:当 的秩为1 B:当 时, 时, 的秩为2 C:当 的秩为2 C:当 时, 时, 的秩为1 D:当 的秩为1 D:当 时, 时, 的秩为2 的秩为2 |
|
设向量组 ,则下列说法错误的是( ) ,则下列说法错误的是( ) |
A:若 中有一个是零向量,则向量组 中有一个是零向量,则向量组 线性相关 B:若 线性相关 B:若 线性无关,则任意向量都不能由其余向量线性表示 C:若 线性无关,则任意向量都不能由其余向量线性表示 C:若 可以由 可以由 线性表示,则表示式必不唯一 D:零向量必可以由 线性表示,则表示式必不唯一 D:零向量必可以由 线性表示 线性表示 |
|
若 阶方阵 阶方阵 可以对角化,则( ) 可以对角化,则( ) |
A: B: B: 一定有 一定有 个互异的特征值 C: 个互异的特征值 C: 一定是对角阵 D: 一定是对角阵 D: 一定有 一定有 个线性无关的特征向量 个线性无关的特征向量 |
|
 |
| A: 充要条件 B:充分条件 C:必要条件 D:既非充分也非必要条件 |
|
 |
A: B: B: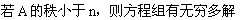 C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: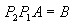 |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 |
| A:1,2,3 B:4,6,12 C:2,4,6 D:8,16,24 |
|
 |
A: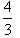 B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
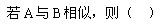 |
A: B: B: C: C: D: D: |
|
 |
A: B: B: C: C: D: D: |
|
 bsp;) bsp;) |
| A:A有n个不同特征值 B:A一定是n阶实对称阵 C:A有n个线性无关的特征向量 D:A的属于不同的特征值的特征向量正交 |
|
 |
A: B: B: C: C: D: D: |
|
求矩阵方程 ,其中 ,其中 ; ; |
|
|
|

