青书学堂河南理工大学计算方法(专升本)网上考试答案
一节点的Gauss-Legendre求积公式计算积分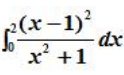 的近似值为( )。 的近似值为( )。 |
| A:0 B:1 C:2 D:3 |
|
积公式 的代数精度为( )。 的代数精度为( )。 |
| A:1 B:2 C:3 D:5 |
|
积公式 的代数精度为( )。 的代数精度为( )。 |
| A:1 B:2 C:3 D:5 |
|
 |
| A:直接法和迭代法 B:直接法和二分法 C:反幂法和乘幂法 D:差分法迭代法 |
|
 运算即可得到方程组的精确解。 运算即可得到方程组的精确解。 |
| A:直接法 B:迭代法 C:差分法 D:高斯消去法 |
|
 行变换。 行变换。 |
| A:差分法 B:反幂法 C:乘幂法 D:高斯消去法 |
|
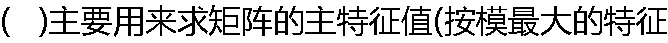 值)及相应的特征向量。 值)及相应的特征向量。 |
| A:反幂法 B:差分法 C:乘幂法 D:直接法 |
|
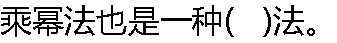 |
| A:差分 B:迭代 C:二分 D:直接法 |
|
 特征向量。 特征向量。 |
| A:反幂法 B:差分法 C:乘幂法 D:二分法 |
|
 特征向量。 特征向量。 |
| A:最小 B:最大 C:任意 |
|
 )。 )。 |
| A:1 B:2 C:3 D:4 |
|
 |
| A:对分法 B:差分法 C:迭代法 D:反幂法 |
|
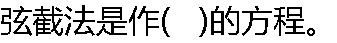 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
 |
| A:切线 B:弦线 C:弧线 D:直线 |
|
 |
| A:节点 B:峰值 C:均值 D:差值 |
|
 。 。 |
| A:差分 B:迭代 C:高斯消去法 D:反幂法 |
|
 |
| A:等距节点插值多项式 B:非等距节点插值多项式 C:插值多项式 D:赛德尔迭代格式 |
|
 速迭代法。 速迭代法。 |
| A:赛德尔迭代格式 B:牛顿迭代格式 C:等距节点插值多项式 D:非等距节点插值多项式 |
|
 |
| A:精确法 B:精准法 C:精度法 D:二分法 |
|
 解”,这说的是以下什么方法的基本思想?( ) 解”,这说的是以下什么方法的基本思想?( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:牛顿迭代法 |
|
“通过计算隔根区间的中点,逐步将隔根区间缩小,从而得方程的近似根数列 ”的是什么方法的基本思想?( ) ”的是什么方法的基本思想?( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
“把方程f(x)=0化为等价方程x=φ(x),得迭代公式 ,用该公式反复迭代,得方程的近似根数列”指的是( ) ,用该公式反复迭代,得方程的近似根数列”指的是( ) |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
 定出隔根区间,或者将方程等价变形为g1(x)=g2(x),画出函数y=g1(x)和y=g2(x)的简图,从两条曲线交点的横坐标的位置确定隔根区间”的方法是( )。 定出隔根区间,或者将方程等价变形为g1(x)=g2(x),画出函数y=g1(x)和y=g2(x)的简图,从两条曲线交点的横坐标的位置确定隔根区间”的方法是( )。 |
| A:描图法 B:逐步搜索法 C:二分法 D:迭代法 |
|
拉格朗日差值多项式中,称 为关于差值基点 为关于差值基点 的差值基函数,则以下各式正确的是。( ) 的差值基函数,则以下各式正确的是。( ) |
A: B: B:   C: C:  D: D:   |
|
若要使用顺序高斯消去法求解方程组 ,顺序消元过程能进行到底的充要条件是系数矩阵A满足( )。 ,顺序消元过程能进行到底的充要条件是系数矩阵A满足( )。 |
A:A的各阶顺序主子式不为零 B: 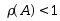 C: C:  D: D:  |
|
已知方程 在 在 内有一实根,现在把方程写成以下两种不同的等价式, 内有一实根,现在把方程写成以下两种不同的等价式, ,对于每个等价式对应的迭代公式在x0=1.5附近的敛散性,下面哪种说法正确?( ) ,对于每个等价式对应的迭代公式在x0=1.5附近的敛散性,下面哪种说法正确?( ) |
| A: (1)发散(2)收敛 B: (1)发散(2)发散 C: (1)收敛(2)收敛 D: (1)收敛(2)发散 |
|
若近似值 精确到 精确到 ,则 ,则 的绝对误差限是( )。 的绝对误差限是( )。 |
A: B: B: C: C: D: D: |
|
| 取3.1415为圆周率π的近似值,则该近似值具有( )位有效数字。 |
| A: 5 B: 4 C: 3 D: 2 |
|
设 ,均差 ,均差 =( ) =( ) |
| A:3 B: 5 C: -6 D:0 |
|
函数 的n次差值多项式 的n次差值多项式 的余项为( )。 的余项为( )。 |
A: B: B: C: C: D: D: |
|
 |
A:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: B:方程x=f(x)的根的牛顿迭代格式为: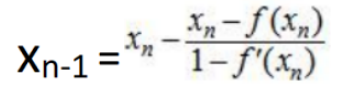 C:x=cosx根的牛顿迭代公式是: C:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: D:x=cosx根的牛顿迭代公式是: |
|
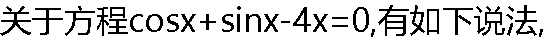 正确的是( )。 正确的是( )。 |
A:该方程的有一个根 B:该方程的有二个根 C:隔根区间为[0,π/4] D:收敛的迭代公式为: |
|
 |
A:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04476 B:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04476 B:用迭代法求 的正根,准确到小数点后第5位的值为:a≈1.04000 C:用迭代法求方程 的正根,准确到小数点后第5位的值为:a≈1.04000 C:用迭代法求方程 的根,要求精度为 的根,要求精度为 的值为:a≈0.0905 D:用迭代法求方程 的值为:a≈0.0905 D:用迭代法求方程 的根,要求精度为 的根,要求精度为 的值为:a≈0.0900 的值为:a≈0.0900 |
|
方程 在1.5附近有根,把方程写成4种不同的等价形式,并建立相应的迭代公式,具体如图,则判断每种迭代公式产生的数列在1.5附近的收敛性,正确的是( )。 在1.5附近有根,把方程写成4种不同的等价形式,并建立相应的迭代公式,具体如图,则判断每种迭代公式产生的数列在1.5附近的收敛性,正确的是( )。
 |
| A:(1)收敛 B:(2)收敛 C:(3)发散 D:(4)发散 |
|
| 取“355/113”作为π的近似值,则下列计算结果正确的是( )。 |
A:绝对误差为: B:相对误差为: B:相对误差为: C:有效数字为:7位 D:有效数字为:6位 C:有效数字为:7位 D:有效数字为:6位 |
|
 |
| A:偏微分方程定解问题的数值解法之一是差分解法 B:偏微分方程定解问题的数值解法之二是有限元方法 C:差分解法的基本思想是:在偏微分方程中,用差商(均差)代替偏导数,把偏微分方程定解问题转化为求解线性代数方程问题,从而得到定解问题的解函数在离散点的近似值 D:线性代数方程称为差分方程,差分方程的解称为偏微分方程定解问题的数值解. |
|
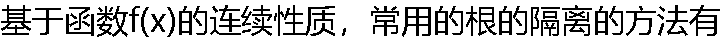 : : |
| A:描图法 B:逐步搜索法 C: 拼图法 D: 逐行搜索法 |
|
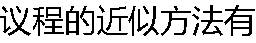 |
| A:二分法 B:迭代法 C:牛顿法 D:弦截法 |
|
 以下答案中那几项是正确的? 以下答案中那几项是正确的? |
A: B: B: C: C: D: D: |
|
| 取“22/7”作为π的近似值,则下列计算结果正确的是( )。 |
A:绝对误差为: B:相对误差为: B:相对误差为: C:有效数字为:3位 D:有效数字为:2位 C:有效数字为:3位 D:有效数字为:2位 |
|
(证明题)
证明方程 在区间[1,2]内有且仅有一个根。并用牛顿迭代法(要求收敛)求根的近似值,五位小数稳定。 在区间[1,2]内有且仅有一个根。并用牛顿迭代法(要求收敛)求根的近似值,五位小数稳定。 |
|
|

