| |
|
QQ:3446094242 |
|
|
微信号:goodluckgold |
|
| 课件学习、网上考试答案,如有需要,请加微信或QQ,全程辅导,为您排忧解难!!! |
|
|
|
|
| |
|
|
青书学堂华北水利水电大学线性代数(专升本)网上考试答案
n维向量 线性无关的充要条件是 ( ) 线性无关的充要条件是 ( ) |
A:存在不全为零的数 ,使 ,使 ; B: ; B: 中任意两个向量都线性无关; C: 中任意两个向量都线性无关; C: 中任意一个向量都不能用其余向量线性表示; D: 中任意一个向量都不能用其余向量线性表示; D: 中存在一个向量,它不能用其余向量线性表示。 中存在一个向量,它不能用其余向量线性表示。 |
|
设 为 为 阶非奇异矩阵 阶非奇异矩阵 , , 为 为 的伴随矩阵,则( ) 的伴随矩阵,则( ) |
A: ; B: ; B: ; C: ; C: ; D: ; D: 。 。 |
|
对于 元齐次线性方程组 元齐次线性方程组 ,以下命题中,正确的是( ) ,以下命题中,正确的是( ) |
A:若 的列向量组线性无关,则 的列向量组线性无关,则 有非零解; B:若 有非零解; B:若 的行向量组线性无关,则 的行向量组线性无关,则 有非零解; C:若 有非零解; C:若 的列向量组线性相关,则 的列向量组线性相关,则 有非零解; D:若 有非零解; D:若 的行向量组线性相关,则 的行向量组线性相关,则 有非零解。 有非零解。 |
|
设 为实矩阵,则线性方程组 为实矩阵,则线性方程组 只有零解是矩阵 只有零解是矩阵 为正定矩阵的( ) 为正定矩阵的( ) |
| A:充分条件; B:必要条件; C:充要条件; D:无关条件。 |
|
已知 为四维列向量组,且行列式 为四维列向量组,且行列式  , ,
 ,则行列式 ,则行列式  ( ) ( ) |
A: ; B:B. ; B:B. ; C: ; C: ; D: ; D: 。 。 |
|
| 设向量α、β的长度依次为2和3,则向量α+β与α-β的内积(α+β,α-β)=( ). |
| A:-10 B:-8 C:-5 D:1 |
|
| 设A是4×6矩阵,R(A)=2,则齐次线性方程组Ax=0的基础解系中所含向量的个数是( ) |
| A:1 B:2 C:3 D:4 |
|
| 设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有( ) |
| A:k≤3 B:k lt;3 C:k=3 D:k gt;3 |
|
设矩阵A= ,A*是A的伴随矩阵,则A *中位于(1,2)的元素是( ) ,A*是A的伴随矩阵,则A *中位于(1,2)的元素是( ) |
| A:–6 B:6 C:2 D:–2 |
|
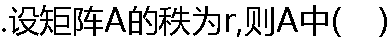 |
| A:所有r-1阶子式都不为0 B:所有r-1阶子式全为0 C:至少有一个r阶子式不等于0 D:所有r阶子式都不为0 |
|
设矩阵A= ,已知α= ,已知α= 是它的一个特征向量,则α所对应的特征值为 ( ). 是它的一个特征向量,则α所对应的特征值为 ( ). |
| A:1 B:2 C:3 D:4 |
|
| 设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是( ) |
A:η1+η2是Ax=0的一个解 B: η1+ η1+ η2是Ax=b的一个解 C:η1-η2是Ax=0的一个解 D:2η1-η2是Ax=b的一个解 η2是Ax=b的一个解 C:η1-η2是Ax=0的一个解 D:2η1-η2是Ax=b的一个解 |
|
已知矩阵 ,伴随矩阵 ,伴随矩阵 ,且 ,且 有非零解,则 ( ) 有非零解,则 ( ) |
A: ; B: ; B: 或 或 ; C: ; C: ; D: ; D: 且 且 。 。 |
|
 为( )。 为( )。 |
| A:1 B:2 C:3 D:4 |
|
| 设A是一个n(≥3)阶方阵,下列陈述中正确的是( ) |
| A:如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量 B:如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值 C:A的2个不同的特征值可以有同一个特征向量 D:如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关 |
|
设矩阵A= ,则A-1等于( ) ,则A-1等于( ) |
A: B: B: C: C: D: D: |
|
 关,则a=( ). 关,则a=( ). |
| A:-10 B:10 C:8 D:9 |
|
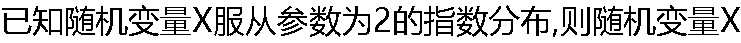 的期望为( ) 的期望为( ) |
A:- B:0 C: B:0 C: D:2 D:2 |
|
设行列式 ,则 ,则 () () |
| A:-6 B:-3 C:3 D:6 |
|
 |
| A:秩(A) lt;n B:秩(A)=n-1 C:A=0 D:方程组Ax=0只有零解 |
|
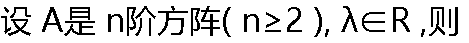 | λA |=λ| A | 。 | λA |=λ| A | 。 |
| A:正确 B:错误 |
|
 价。 价。 |
| A:正确 B:错误 |
|
 一定有无穷多解。 一定有无穷多解。 |
| A:正确 B:错误 |
|
 应的关系。 应的关系。 |
| A:正确 B:错误 |
|
 ( ) ( ) |
| A:正确 B:错误 |
|
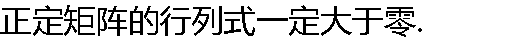 ( ) ( ) |
| A:正确 B:错误 |
|
设 是 是 阶矩阵, 则 阶矩阵, 则 . ( ) . ( ) |
| A:正确 B:错误 |
|
 ( ) ( ) |
| A:正确 B:错误 |
|
 ( ) ( ) |
| A:正确 B:错误 |
|
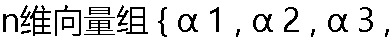 α 4 } 线性相关,则 { α 2 , α 3 , α 4 } 线性无关。 α 4 } 线性相关,则 { α 2 , α 3 , α 4 } 线性无关。 |
| A:正确 B:错误 |
|
计算四阶行列式
 |
|
|
求矩阵 的逆矩阵. 的逆矩阵. |
|
|
|

