青书学堂黄河水利职业技术学院高等数学(高起专)网上考试答案
若  二次可导,是奇函数又是周期函数,则下述命题成立的是_(1)_ 二次可导,是奇函数又是周期函数,则下述命题成立的是_(1)_ |
A: 是奇函数又是周期函数 ; B: 是奇函数又是周期函数 ; B: 是奇函数但不是周期函数; C: 是奇函数但不是周期函数; C: 是偶函数且是周期函数 ; D: 是偶函数且是周期函数 ; D: 是偶函数但不是周期函数. 是偶函数但不是周期函数. |
|
设  ,且在点 ,且在点  的某邻域中(点 的某邻域中(点  可除外), 可除外),  及 及  都存在,且 都存在,且  ,则 ,则  存在是 存在是  存在的( ). 存在的( ). |
| A:充分条件; B:必要条件; C:充分必要条件; D:既非充分也非必要条件 . |
|
对于函数  点 点  _(1)_ _(1)_ |
| A:不是驻点; B:是驻点却非极值点; C:是极小值点; D:是极大值点. |
|
函数   是( ). 是( ). |
| A:偶函数; B:奇函数; C:非奇非偶函数; D:不能断定. |
|
设  是奇函数,且 是奇函数,且  ,则 _(1)_ ,则 _(1)_ |
A: 是 是 的极小值点; B: 的极小值点; B: 是 是 的极大值点; C: 的极大值点; C: 在 在 的切线平行于 的切线平行于 轴; D: 轴; D: 在 在 的切线不平行于 的切线不平行于 轴 轴 |
|
当  很小时, 很小时,  ( ) ( ) |
A: ; B: ; B: ; C: ; C: ; D: ; D: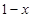 . . |
|
若在  内,函数 内,函数  的一阶导数 的一阶导数  ,二阶导数 ,二阶导数  ,则函数 ,则函数  在此区间内( ). 在此区间内( ). |
| A:单调减少,曲线是凹的; B:单调减少,曲线是凸的; C:单调增加,曲线是凹的; D:单调增加,曲线是凸的. |
|
函数  在 在  处连续是函数在 处连续是函数在  可微的( ) 可微的( ) |
| A:必要条件; B:充分条件; C:充要条件; D:既非充分又非必要条件. |
|
已知无界区域上的二重积分  收敛,则m的取值范围为( ) 收敛,则m的取值范围为( ) |
A: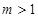 ; B: ; B: ; C: ; C: ; D: ; D: . . |
|
函数  的定义域为( ). 的定义域为( ). |
A: ; B: ; B: ; C: ; C: ; D: ; D: . . |
|
设  ,则 ,则  等于 _(1)_ 等于 _(1)_ |
A: ; B: ; B: ; C: ; C: ; D: ; D: . . |
|
设  ,则 _(1)_ ,则 _(1)_ |
A:数列 收敛; B: 收敛; B: ; C: ; C: ; D:数列 ; D:数列 可能收敛,也可能发散。 可能收敛,也可能发散。 |
|
当  时, 时,  是( ). 是( ). |
A:比 高阶无穷小; B:比 高阶无穷小; B:比 低阶无穷小; C:与 低阶无穷小; C:与 同阶无穷小; D:与 同阶无穷小; D:与 等价无穷小. 等价无穷小. |
|
 是函数 是函数  的_(1)_ 的_(1)_ |
| A:可去间断点; B:跳跃间断点; C:第二类间断点; D:连续点. |
|
点(0,0)是曲线  的 ( ) 的 ( ) |
| A:极大值点; B:极小值点 ; C:拐点 ; D:使导数不存在的点. |
|
若  在 在  可导且 可导且  ,则_(1)_ ,则_(1)_ |
A:至少存在一点 ,使 ,使 ; B:一定不存在点 ; B:一定不存在点 ,使 ,使 ; C:恰存在一点 ; C:恰存在一点 ,使 ,使 ; D:对任意的 ; D:对任意的 ,不一定能使 ,不一定能使 . . |
|
幂级数  的收敛区间是( ), 的收敛区间是( ), |
A: ; B: ; B: ; C: ; C: ; D: ; D: |
|
点  是函数 是函数  的( ). 的( ). |
| A:连续点; B:可去间断点; C:跳跃间断点; D:第二类间断点. |
|
设  则 则  ( ) ( ) |
A: ; B: ; B: ; C: ; C: ; D: ; D: . . |
|
极限  _(1)_ _(1)_ |
A:e ; B:1; C: ; D: ; D: . . |
|
设 ,则 ,则 ( ) ( ) |
A: ? B: ? B: ? C: ? C: ? D: ? D: ? |
|
设函数 ,则 ,则 ( )。 ( )。 |
A: 0 ; B: 1 ; C: ? ?; D: ? ?; D: ? ?。 ?。 |
|
设函数 在区间 在区间 内满足 内满足 且 且 ,则函数在此区间内是( )。 ,则函数在此区间内是( )。 |
| A: 单调减少且凹的; B: 单调减少且凸的; C: 单调增加且凹的; D: 单调增加且凸的。 |
|
设 ,则 ,则 是 是 在 在 上的( )。 上的( )。 |
| A: 极小值点,但不是最小值点; B: 极小值点,也是最小值点; C: 极大值点,但不是最大值点; D: 极大值点,也是最大值点。 |
|
设函数 在 在 上连续,且在 上连续,且在 内 内 ,则下列不等式成立的是( )。 ,则下列不等式成立的是( )。 |
A: ? ?; B: ? ?; B: ? ?; C: ? ?; C: ? D: ? D: ? |
|
设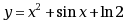 ,则 ,则 ( )。 ( )。 |
A: ? ?; B: ? ?; B: ? ?; C: ? ?; C: ? ?; D: ? ?; D: ? ?。 ?。 |
|
设函数 ,则 ,则 ( ) ( ) |
A: ? B: ? B: ? C: ? C: ? D: ? D: ? |
|
设 , , ,则当 ,则当 时( )。 时( )。 |
A: ? 与 与 是同阶但不等价的无穷小; B: ? 是同阶但不等价的无穷小; B: ? 与 与 是等价的无穷小; C: ? 是等价的无穷小; C: ? 是 是 的高阶无穷小; D: ? 的高阶无穷小; D: ? 是 是 的低阶无穷小。 的低阶无穷小。 |
|
已知 存在,则 存在,则 的正确结果是( )。 的正确结果是( )。 |
A: ? B: ? B: ? C: ? C: ? D: ? D: ? |
|
函数y=f(x),在 处,下列结论正确的是( ) 处,下列结论正确的是( ) |
A: 若函数在 处连续,则函数在该点一定可导。 B: 若函数在 处连续,则函数在该点一定可导。 B: 若函数在 处可导,则函数在该点一定连续。 C: 若函数在 处可导,则函数在该点一定连续。 C: 若函数在 处不可导,则函数在该点一定不连续。 D: 函数的连续与函数的可导是等价关系。 处不可导,则函数在该点一定不连续。 D: 函数的连续与函数的可导是等价关系。 |
|
函数  f(x) 在[ a,b ] 上可积的必要条件是 f(x) 在[ a,b ] 上可积的必要条件是 |
| A:连续 B:有界 |
|
| 函数 Z=f(x,y)在 (x。y。)处连续是函数在(x。y。)可微的必要条件 |
| A:正确 B:错误 |
|
二重积分 ,若积分区域为 ,若积分区域为 ,则该二重积分结果为 ,则该二重积分结果为 。( ) 。( ) |
| A:正确 B:错误 |
|
 , , 是直线 是直线 从(0,0)到(1,1)一段弧; 从(0,0)到(1,1)一段弧; , , 是 是 上从(0,0)到(1,1)上的一段弧,则 上从(0,0)到(1,1)上的一段弧,则 , ,  。 ( ) 。 ( ) |
| A:正确 B:错误 |
|
 的通解是 的通解是 。若 。若 , , ,则特解是 ,则特解是 。( ) 。( ) |
| A:正确 B:错误 |
|
二次曲面 的图形是半径为1的圆柱面。设D由 的图形是半径为1的圆柱面。设D由 所围,则 所围,则 的取值范围是 的取值范围是 。( ) 。( ) |
| A:正确 B:错误 |
|
已知空间点 和平面 和平面 ,则空间点到平面的距离 ,则空间点到平面的距离 = = 。 ( ) 。 ( ) |
| A:正确 B:错误 |
|
方程 表示的曲面是 表示的曲面是  ,其中心坐标是 ,其中心坐标是 。 ( ) 。 ( ) |
| A:正确 B:错误 |
|
已知平面方程 ,则法矢量n= ,则法矢量n= ,若坐标原点在该平面内,则 ,若坐标原点在该平面内,则 。 ( ) 。 ( ) |
| A:正确 B:错误 |
|
空间直角坐标系分为八个卦限,空间点 在第四卦限。( ) 在第四卦限。( ) |
| A:正确 B:错误 |
|
计算定积分 ? ? |
|
|

