青书学堂信阳师范大学数学历史与文化网上考试答案
 |
| A:纳皮尔 B:布里格斯 C:斯蒂弗尔 D:比尔吉 |
|
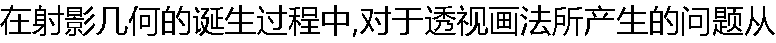 数学上直接给予解答的第一个人是( ) 数学上直接给予解答的第一个人是( ) |
| A:达·芬奇; B:笛卡儿; C:德沙格; D:牛顿 |
|
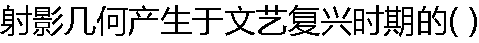 |
| A:音乐演奏 B:服装设计 C:雕刻艺术 D:绘画艺术 |
|
 |
| A:笛卡尔和费马等 B:德沙格和帕斯卡等 C:庞斯列和斯坦纳等 D:施陶特和默比乌斯等 |
|
 数学问题的数学家是( ) 数学问题的数学家是( ) |
| A:希尔伯特 B:庞加莱 C:罗素 D:克莱因 |
|
 |
| A:高斯 B:欧拉 C:魏尔斯特拉斯 D:柯西 |
|
| 1900?年,德国数学家希尔伯特在巴黎国际数学家大会上提出的著名数学问题共有( )。 |
| A:18?个 B:23?个 C:32?个 D:40?个 |
|
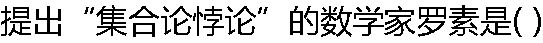 |
| A:英国数学家; B:法国数学家; C:德国数学家; D:巴西数学家 |
|
 中黎曼几何的特例,其中“罗巴契夫斯基非欧几何”对应的情形是( ) 中黎曼几何的特例,其中“罗巴契夫斯基非欧几何”对应的情形是( ) |
| A:曲率为正常数 B:曲率为负常数 C:曲率恒等于零 D:曲率不存在 |
|
 ) ) |
| A:俄国人 B:德国人 C:葡萄牙人 D:匈牙利人 |
|
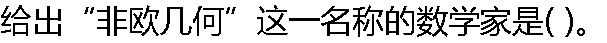 |
| A:高斯 B:罗巴契夫斯基 C:波约; D:黎曼 |
|
 作者是( )。 作者是( )。 |
| A:高斯 B:罗巴契夫斯基 C:波约 D:黎曼 |
|
 其发现者是( )。 其发现者是( )。 |
| A:伽利略 B:哥白尼 C:开普勒 D:牛顿 |
|
1593法国( )给出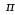 的第一个解析表达式。 的第一个解析表达式。 |
| A:韦达 B:帕斯卡 C:笛卡儿 |
|
公元263年刘徽注( )用割圆术求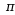 ,包含极限的思想。 ,包含极限的思想。 |
| A:《孙子算经》 B:《几何原本》 C:《九章算术》 |
|
 认为是古希腊数学的安魂曲,其作者为( )。 认为是古希腊数学的安魂曲,其作者为( )。 |
| A:托勒玫 B:帕波斯 C:阿波罗尼奥斯 D:丢番图 |
|
 微的函数例子,这位数学家是( )。 微的函数例子,这位数学家是( )。 |
| A:高斯 B:波尔查诺 C:魏尔斯特拉斯 D:柯西 |
|
| 发现著名公式e iθ =cosθ +isinθ 的是( )。 |
| A:笛卡尔 B:牛顿 C:莱布尼茨 D:欧拉 |
|
 |
| A:《曲线求积术》; B:《流数术》; C:《现代微积分学》; D:《自然哲学的数学原理》 |
|
 也是相互独立的,但在发表的时间上( ) 也是相互独立的,但在发表的时间上( ) |
| A:牛顿先于莱布尼茨 B:莱布尼茨先于牛顿 C:牛顿和莱布尼茨同时 D:谁先谁后尚未定论 |
|
 |
| A:求曲线的切线; B:求瞬时变换率; C:求函数的极大极小值 D:用无穷小过程计算特殊形状的面积 |
|
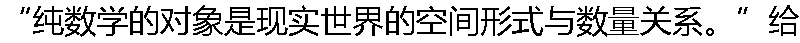 出这个关于数学本质的论述的人是( ) 出这个关于数学本质的论述的人是( ) |
| A:笛卡尔 B:恩格斯 C:康托 D:罗素 |
|
 的解析表达式。”这个函数定义在18世纪后期占据了统治地位,给出这个函数定义的数学家是( ) 的解析表达式。”这个函数定义在18世纪后期占据了统治地位,给出这个函数定义的数学家是( ) |
| A:莱布尼茨 B:约翰·贝努利 C:欧拉 D:狄利克雷 |
|
 |
| A:欧拉 B:韦达 C:柯西 D:莱布尼茨 |
|
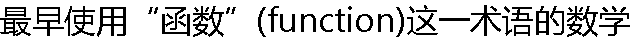 家是( )。 家是( )。 |
| A:莱布尼茨 B:约翰·贝努利 C:雅各布·贝努利 D:欧拉 |
|
 |
| A:中国的《九章算术》 B:阿拉伯花拉子米的《代数学》 C:卡尔丹的《大法》 D:牛顿的《普遍算术》 |
|
 |
| A:纸草书上 B:竹片上 C:木板上 D:泥板上 |
|
 |
| A:纸草书 B:羊皮书 C:泥版 D:金字塔内的石刻 |
|
 |
| A:埃及纸草书和苏格兰纸草书 B:莱茵德纸草书和莫斯科纸草书 C:莫斯科纸草书和希腊纸草书 D:莱茵德纸草书和尼罗河纸草书 |
|
 锥曲线理论。( ) 锥曲线理论。( ) |
| A:正确 B:错误 |
|
 派,包括以罗素为代表的形式主义、以布劳威尔为代表的直觉主义和以希尔伯特为代表的逻辑主义。( ) 派,包括以罗素为代表的形式主义、以布劳威尔为代表的直觉主义和以希尔伯特为代表的逻辑主义。( ) |
| A:正确 B:错误 |
|
 莱布尼茨,他是德国数学家。( ) 莱布尼茨,他是德国数学家。( ) |
| A:正确 B:错误 |
|
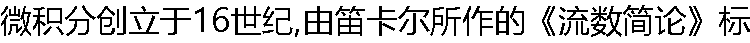 志着微积分的诞生。( ) 志着微积分的诞生。( ) |
| A:正确 B:错误 |
|
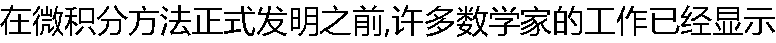 着微积分的萌芽,如开普勒的无穷算术、巴罗的旋转体体积计算以及沃利斯的微分三角学等。( ) 着微积分的萌芽,如开普勒的无穷算术、巴罗的旋转体体积计算以及沃利斯的微分三角学等。( ) |
| A:正确 B:错误 |
|
 |
| A:正确 B:错误 |
|
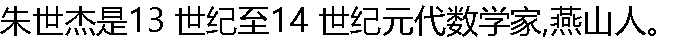 代表著作是《四元玉鉴》,其主要数学成就是求解方程的四元术、高阶等差数列研究及其在内插法上的应用。( ) 代表著作是《四元玉鉴》,其主要数学成就是求解方程的四元术、高阶等差数列研究及其在内插法上的应用。( ) |
| A:正确 B:错误 |
|
 》发表论文“模曲线和费马最后定理” 标志着费马大定理证明的最后完成。 》发表论文“模曲线和费马最后定理” 标志着费马大定理证明的最后完成。 |
| A:正确 B:错误 |
|
 》和《印度的计算术》。( ) 》和《印度的计算术》。( ) |
| A:正确 B:错误 |
|
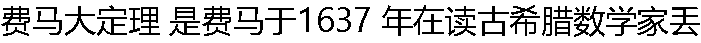 番图的《算术》一书时,给出的猜想。( ) 番图的《算术》一书时,给出的猜想。( ) |
| A:正确 B:错误 |
|
 了数学史上的第一次数学危机。( ) 了数学史上的第一次数学危机。( ) |
| A:正确 B:错误 |
|
 严格的证明。 ( ) 严格的证明。 ( ) |
| A:正确 B:错误 |
|
 立于15世纪。( ) 立于15世纪。( ) |
| A:正确 B:错误 |
|
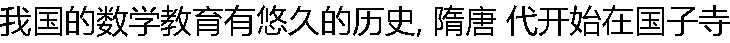 里设立“算学”,唐至五代 代则在科举考试中开设了数学科目,叫“明算科”。 ( ) 里设立“算学”,唐至五代 代则在科举考试中开设了数学科目,叫“明算科”。 ( ) |
| A:正确 B:错误 |
|
 础上创立了相当完美的圆锥曲线理论,其著作《几何基础》代表了希腊演绎几何的最高成就。 ( ) 础上创立了相当完美的圆锥曲线理论,其著作《几何基础》代表了希腊演绎几何的最高成就。 ( ) |
| A:正确 B:错误 |
|
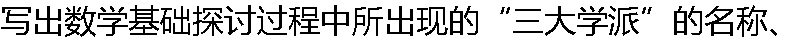 代表人物、主要观点。 代表人物、主要观点。 |
|
|
| 证明了π的超越性,从而确立了化圆为方不可能性的数学家是( ) |
| A:旺泽尔 B:牛顿 C:伽罗瓦 D:林德曼 |
|

